計算理論(P vs NP問題, NP完全性)

P vs NP問題

これまでにPはその言語に属しているかどうかを多項式時間で判定できる言語のクラス, NPはその言語に属してことを多項式時間で検証できる言語のクラスだと学んできた.

P ≠ NPだと多くの人が県警から信じているが, 実際にPに属していないNPの言語は見つかっていない. 多項式時間で判定できないことを証明するのは難しい. もしかしたら良いアルゴリズムが存在するかもしれない.

NPに属する問題の中で最も難しい問題を見つけようというアプローチ. この最も難しい問題をNP完全問題と呼ぶ.

NP完全問題は最も難しい問題なのでPに属さないことを証明するのが比較的容易なはず. 逆に, 最も難しい問題であるNP完全問題がPに属すればP = NPとなることがわかる.

問題Aへの入力を問題Bへの入力に変換することを考える. この変換(帰着という)が存在するならば, 問題Bを解くアルゴリズムを用いて, 問題Aも解けることになる. Aへの任意の入力を帰着を用いてBへの入力へと変換し, Bを解くアルゴリズムに入力すれば問題を解くことが可能.

例えば, 長方形の面積を求める問題は, 辺の高さと幅を求める問題に帰着可能. 連立方程式を解く問題は, 逆行列を求める問題へと帰着可能.

任意の入力 $w$ に対してテープに $f(w)$ だけを書き込んで停止し, その動作時間は多項式時間であるようなTuring機械が存在するとき, 関数fは多項式時間計算可能関数であるという.

言語Aと言語Bに対して, 多項式時間計算可能 $f$ が存在して, 全ての $w$ について $w ∈ A ⇔ f(w) ∈ B$ であるとき, $A ≦_p B$ と書き, 言語Aが言語Bに多項式時間帰着可能であるという.

次の条件を満たすBをNP完全という.

わかりやすく言うと, NPに属する全ての問題はNP完全よりも同等か優しい. ということ.

4色問題の紹介. どう計算理論と絡んでくるのかよくわからない.

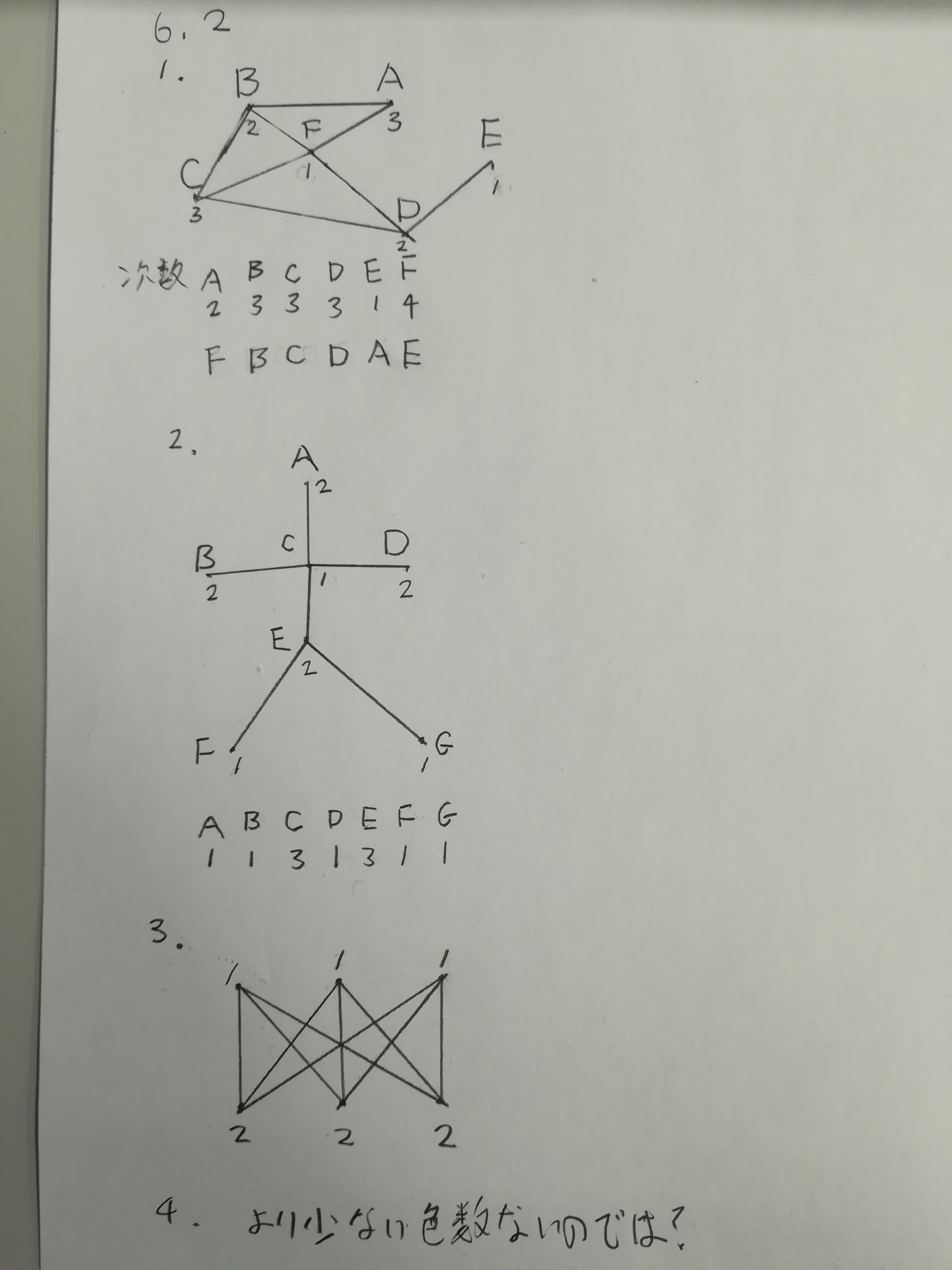
Welsh-Powellのアルゴリズムの記憶を思い出した.